Main Research Publications People Photos Links Supporters  Collaborators

Spatiotemporal Salience via Centre-Surround Comparison of Visual Spacetime Orientations

Contributors

  • Andrei Zaharescu
  • Richard P. Wildes

Overview

Early delineation of the most salient portions of a temporal image stream (e.g., a video) could serve to guide subsequent processing to the most important portions of the data at hand. Toward such ends, the present paper documents an algorithm for spatiotemporal salience detection. The algorithm is based on a definition of salient regions as those that differ from their surrounding regions, with the individual regions characterized in terms of 3D, (x,y,t), measurements of visual spacetime orientation. The algorithm has been implemented in software and evaluated empirically on a publically available database for visual salience detection. The results show that the algorithm outperforms a variety of alternative algorithms and even approaches human performance.

Introduction

Motivation

  • Temporal image streams (e.g., videos) are notorious for the vast amounts of data they comprise.
  • The efficient processing of such data would benefit greatly from early delineation of the most salient portions of the data.

Challenges

  • Accurately distinguish salient regions in a temporal image stream from backgrounds across a wide range of real world situations.
  • Operate without reliance on a priori models of targets of interest or backgrounds to be disregarded.

Contributions

  • A novel, algorithmic approach for spatiotemporal salience detection is presented based on centre-surround differences in spacetime oriented structure.
  • The approach defines salient regions as those that differ from their surrounding neighborhood in terms of the dynamics of their particular image streams and thereby does not require a priori models of targets or backgrounds.
  • A software implementation has been evaluated in comparison to seven alternatives and shows best overall performance, even approaching that of humans.

Technical Approach

Overview

  • Salient regions are defined as those that differ from their surrounding neighborhood in terms of the spacetime structure of their particular image streams.
  • Computational realization of this principle entails specification of two matters:
    • A base representation for characterizing visual spacetime structure must be defined: Pixelwise distributions of visual spacetime, (x; y; t), orientation measurements serve this role.
    • A quanitification of the difference in centre vs. surround regions must be specified: Local measurements are aggregated over centre and surround; the Kullback-Leibler divergence compares the two.

Base Representation

  • In the developed approach to salience detection, visual spacetime structure is represented in terms of local distributions of multiscale 3D, (x,y,t), spacetime orientation measurements.
  • This representation is advantageous as it provides a uniform way to capture both spatial and dynamic image properties: Orientations that lie along (x,y)-planes capture spatial pattern; orientations that extend into the temporal dimension, t, capture dynamics.

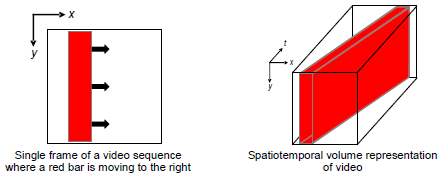
  • For this work, filtering was performed using broadly tuned, steerable, separable filters based on the third derivative of a Gaussian Hence, a measure of local spatiotemporal oriented energy (SOE), E, can be computed according to
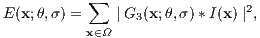    (1)
    where
    • I(x) is the image sequence,
    • G3(x;θ,σ) is the third derivative of 3D Gaussian filter,
    • θ represents the direction of the filter's axis of symmetry,
    • σ represents the scale,
    • x=(x,y,t) represents the spacetime coordinates,
    • Ω is an aggregation region,
    • * symbolizes convolution.
  • To provide robustness to local image intensity contrast that is not indicative of spacetime orientation, the initial measurments are pointwise normalized divided by the sum of their consort,
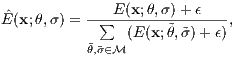    (2)
    where
    • M = σ x θ denotes the set of multiscale oriented energies,
    • ~ denotes variables of summation,
    • ε is a constant introduced as both a noise floor and to avoid instabilities where the overall energy is small.
  • The current approach uses 10 orientations, selected to span the space of orientations for the order of employed filters, and 3 scales.

Centre-Surround Comparison

  • Given the defined measurements of spacetime structure, (2), it is necessary to aggregate the locally defined Ê(x;θ,σ) over centre and surround regions to allow for subsequent comparisons.
  • At any given point, x, a central spacetime support region, C, is defined, using a radius rC.
  • Similarly, at each point a surround support region, S, is defined using a radius rS, extending beyond, but excluding, C.
  • To calculate the centre distribution, ÊC(x;θ,σ), let Ω = C in (1).
  • To calculate the surround distibution, ÊS(x;θ,σ), let Ω = S in (1).
  • The two aggregated distributions are compared by calculating their Kullback-Leibler divergence, as it provides a principled approach based on relative entropy. Thus, salience, ρ(x), is defined as

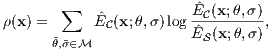    with larger values of ρ taken as indicative of greater spatiotemporal salience.

Empirical Evaluation

Dataset and Experimental Protocol

The proposed SOE algorithm has been evaluated on the USC dataset, containing 50 challenging real-world videos groundtruthed for salience with respect to human fixations. The protocol is to use the Kulback-Leibler divergence to compare algorithm recovered salience at human fixated points vs. randomly sampled points.

Quantitative Results

Comparative quantitative results for the proposed SOE algorithm and seven alternatives show that SOE achieves best overall performance. The SOE KL divergence of 0.624 significantly tops the previous top performer (AIM) and approaches human performance, KL divergence of 0.679 ± 011. The alternative algorithms include the best performing single image measure reported elsewhere, local Entropy [Itti et al. 2009], centre-surround comparisons of temporal Flicker [Itti et al. 2009], Motion [Itti et al. 2009] and a combination of features (colour, 2D spatial orientation, motion and flicker) centre-surround Saliency [Itti et al. 2009], Outliers and Bayesian Surprise in the same feature combination [Itti et al. 2009] and Attention by Information Maximization (AIM) [Bruce et al. 2009]. It is seen that the proposed approach (SOE) outperforms all the alternative approaches by a significant margin (i.e., beyond the standard deviation separations).

Name KL Score
Entropy 0.151 ± 0.005
Flicker 0.179 ± 0.005
Motion 0.204 ± 0.005
Outliers 0.204 ± 0.006
Name KL Score
Saliency 0.205 ± 0.006
Surprise 0.241 ± 0.006
AIM 0.328 ± 0.009
SOE 0.624 ± 0.012


Histogram of SOE salience at eye-fixations locations (blue) vs. random (green) locations is shown below.

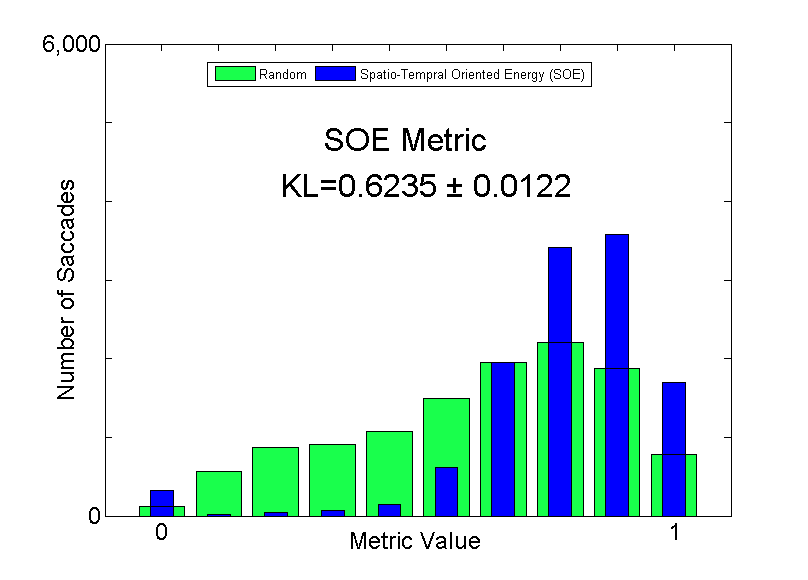
Image Based Results

Image based results indicate that the SOE algorithm typically provides largest values at intuitively reasonable locations, e.g., foreground moving objects. In comparison to human fixations, the algorithm is less conservative and selects a superset of human selected locations.

beverly03 gamecube18 tv-ads05 tv-music01 tv-news04
Image
Image
Image
Image
Image
Image
Image
Image
Image
Image
Image
Image
Image
Image
Image
Top row: Example image frames from the USC dataset. Middle row: Algorithmically derived salience maps. Bottom row: Human fixation-based salience maps.

Additional example input images and algorithmically recovered saliency maps for each of the 50 video clips in the USC dataset are available in the related publication.

Summary

  • A novel algorithm for spatiotemporal salience detection based on centre-surround differences of spatiotemporal oriented energy (SOE) is proposed.
  • In empirical evaluation the algorithm outperforms a variety of state-of-the-art alternatives and even approaches human level performance.

Related Publications
π