Main Research Publications People Photos Links Supporters  Collaborators

Early Spatiotemporal Grouping with a Distributed Oriented Energy Representation

Contributors

  • Konstantinos G. Derpanis
  • Richard P. Wildes

Spatiotemporal grouping. Input video (left) captures a complex scene: In the central region, a person moves rightward behind a chain-link fence to yield (pseudo-) transparency; a second person to the right of the first person moves rightward in front of the fence to yield a single dominant motion; at the available resolution of the image data, the facial regions have little spatial variation and thereby yield unstructured regions; a windblown plant occupies the left area to yield a scintillating pattern; the remaining region made up of the fence and varying background yields a static pattern. The output region grouping (right) accurately indicates the five major structural regions (transparency, single motion, scintillation, static and unstructured) as five different grey-levels.

Overview

Processing of temporal image sequences can be facilitated by an early grouping of the visual data into coherent spacetime regions. Operations that can benefit from such an organization include target recognition and tracking, parametric motion analysis, video indexing, compression and coding. For all of these cases, delineated groupings serve to define support regions that can be processed as wholes for compact and efficient characterization.

In this research a new representation for grouping raw image data into a set of coherent spacetime regions is proposed. This representation supports a unified approach to analyzing a wide range of naturally occuring spatiotemporal phenomena. In particular, the representation describes the presence of particular oriented spacetime structures in a distributed manner. This representation is combined with a standard grouping mechanism (mean-shift) to realize spacetime groupings. Empirical evaluation of the grouping method on synthetic and challenging natural imagery suggests its efficacy.

Challenge

A key challenge to spatiotemporal grouping arises from the wide range of naturally occurring phenomena that must be encompassed. Examples of such phenomena include, motion (single motion and static/no motion), temporal flicker, multiple superimposed motions (transparency, pseudo-transparency, translucency) and dynamic/stochastic texture (scintillation). Critically, motion encompasses only a subset of the spatiotemporal patterns that must be captured in grouping that is widely applicable to imagery of the natural world. Extant approaches deal with such diversity on a case-by-case basis, with motion predominant. Indeed, it appears that no single previous approach to spatiotemporal grouping can be applied with success to a wide range of natural phenomena. The goal of the present work is the development of a unified approach to spatiotemporal grouping that is broadly applicable to the diverse phenomena encountered in the natural world.

Representation: Distributed spatiotemporal orientation

It is proposed that the choice of representation is the key to meeting this challenge: If the representation cannot adequately characterize and distinguish the patterns of interest, then no subsequent grouping algorithm will make the appropriate delineations.

In our work, local spatiotemporal orientation is of fundamental descriptive power, as it captures the first-order correlation structure of the data irrespective of its origin (i.e., irrespective of the underlying visual phenomena) and captures significant, meaningful aspects of its temporal variation (e.g., static vs. moving vs. unstructured) [Wildes and Bergen, 2000]. Correspondingly, visual spacetime is represented according to its local 3D, (x, y, t), orientation structure. In particular, each point of spacetime will be associated with a distribution of measurements that indicates the relative presence of a particular set of spatiotemporal orientations. We capture local spacetime orientation via application of a bank of 3D, steerable, separable oriented energy filters to input video data [Derpanis and Gryn, 2005]. Additional normalization steps are introduced to the oriented energy outputs to avoid spurious segregation due to spatial appearance.

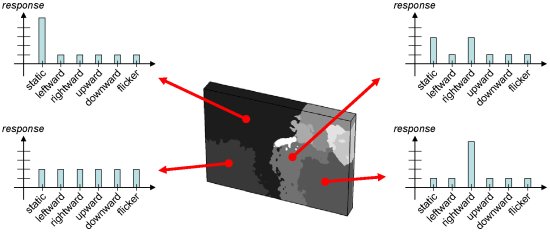Distributed representation of visual spacetime. The grouping result (centre) is taken from above. Each image location carries a distribution representing the degree that the local spacetime structure is consistent with a particular 3D spatiotemporal orientation. The central region of the input, corresponding to transparency, gives rise to two peaks (moving object and static pseudo-transparent foreground); whereas the rightmost region of the input, corresponding to a single moving object, gives rise to a single peak. The leftmost bottom region, corresponding to scintillation, gives rise to a uniform distribution. The facial regions, being devoid of discernable pattern structure at the available resolution, give rise to near zero responses (not shown). The region not attributed to the people or plant, corresponding to static, yields a single peak.

Under this representation, coherency of spacetime is defined in terms of consistent patterns across the decomposition. A contiguous region of spacetime might be grouped on the basis of it giving rise to a significant response in only one component of the decomposition, corresponding to a particular single orientation (e.g., motion); another region might be grouped because it gives rise to significant responses in multiple components of the decomposition, corresponding to transparency-based superposition; yet another region might be grouped as significant, approximately equal magnitude responses arise across all bands of the decomposition, corresponding to scintillation. Sill other regions might arise as they are distinguished by their lack of local structure.

To realize spacetime groupings, we have combined the distributed spacetime orientation representation with a standard grouping mechanism, mean-shift. The overall resulting approach to spatiotemporal grouping is illustrated in the figure below.

Overall approach to spatiotemporal analysis. (left) An image sequence serves as input. (middle) Application of energy filters decomposes the input into a distributed representation according to 3D, (x, y, t), spatiotemporal orientation. The example filter outputs are selective for (left-to-right) flicker (purely temporal variation in image brightness), static (no motion) and rightward (motion) spacetime structure. (right) A grouping process operates across the representation to coalesce regions of common spatiotemporal orientation distributions. The output region grouping (right) accurately indicates the five major structural regions (transparency, single motion, scintillation, static and unstructured) as five different grey-levels.

Results

The performance of our approach to recovering coherent spacetime structure regions has been evaluated on a set challenging natural image data against hand labeled boundary ground truth. Challenging aspects of the dataset include, unstructured regions, regions exhibiting significant temporal aliasing due to motion and the presence of superimposed and non-coherent motion structures, such as transparency and scintillation.

Example 1: A duck swimming (motion structure) over turbulent water (dynamic texture structure).

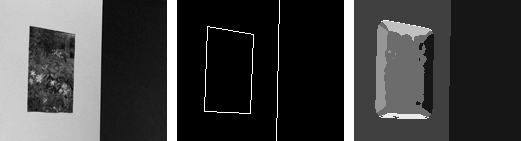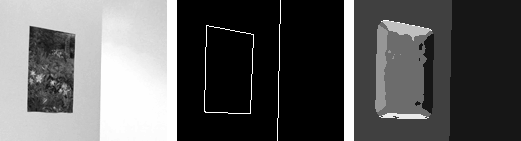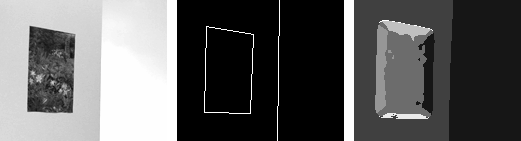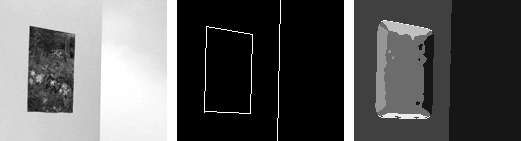Example 2: A painting (static structure) hanging on a blank wall (unstructured) with a light flickering in an adjacent hallway (temporal flicker structure). Salient 1D boundaries along painting frame correspond to aperture problem structure..

Example 3: A person walking behind a fence (pseudo-transparency structure) with a stationary surround of fence, grass and trees (static structure).

Performance has been quantified on a set of 10 videos by sweeping Precision/Recall curves as a function of the grouping method's parameters. Overall, high precision and recall observed in experiments indicate that the combination of the representation and grouping mechanism captures salient image structure while not exhibiting significant over-segmentation.

Additional datasets and results are available at our dataset page.

Related Publications
π